フィッシャーの正確確率検定 エクセル 関数 307481

であるかどうかを検定する方法として，簡単な「二項検定」(Binary test) が使われます。たとえばコインを10 回投げて8 回「表」が現れたとします。 このことがどのような確率になるかを二項確率の関数式Bin で求めると （→「確率」）3 Bin(x, n, p) = Bin(8, 10, 05Excelで行う場合（フィッシャーの正確確率検定の関数がないので，次のように計算式で埋めて行く） ①： 16 C 9 × 13 C 3 ②： 16 C 10 × 13 C 2 ③： 16 C 11 × 13 C 1 ④： 16 C 12 × 13 C 0 片側小計3,955,068 総計 29 C 12 =51,5,935 エクセルを使って、フィッシャーの正確確率検定(2x2)を行いたいと思っています。 たとえば、 アンケート総数 男 10人 女 00人 の中で、 犯罪歴 男 5人 女 1人 という回答が得られた場合、 男女間で犯罪を犯している確率に有意差はあるかどうかを調べるに

統計 Fisher S Exact Test こちにぃるの日記

フィッシャーの正確確率検定 エクセル 関数

フィッシャーの正確確率検定 エクセル 関数-NxM分割表の正確確率検定 NxM表で行と列とに関係がないことを帰無仮説とした検定は、NxM表の正確確率検定である Rで2x2表の検定関数を作成する にて、2x2表の正確確率検定の仕組みを理解し、その仕組みに沿って、検定関数の作成ができることを前提に Pearsonのカイ2乗検定とクロス集計は、IBM SPSS Statisticsの基本ソフトであるBaseのみで実行可能ですが、Fisherの正確確率検定に対応するのはExact Testsオプションです（2×2クロス集計表のみBaseで対応しています）。Exact Testsは、データが少ない場合の正確な検定

遺伝統計学 夏の学校 大阪大学17講義資料 統計学入門

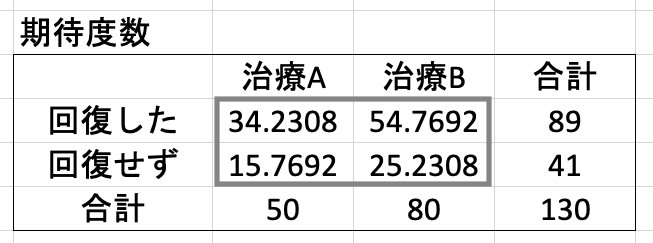
 EZRのFisherの正確検定の関数でオッズ比を計算すると、通常のオッズ比と異なる数値が計算される。 これはなぜなのか？ どう考えたらよいか？ EZRのFisherの正確検定を使わないオッズ比の計算 EZRのFisherの正確検定を使った場合のオッズ比の計算 EZRのFisherの正確検定で使っているオッズ比の計算 手順 最初に下図の表を作成します。 期待値通りに全員にあたりが出たとします。 H2セルに下記の数式を入力します。 数式を確定すると、H2セルには、"1" が表示されます。 期待値と観測値が全く同じため、適合度は100%となります。 続いて、条件をフィッシャーの正確確率検定 エクセル 33フィッシャーの正確確率検定 エクセル 関数 Fisher正確確率検定の数式には階乗が用いられる．このため，EXCELで計算しようとするとコンピューターがオーバーフローしてしまうため，解析ソフトを使用し

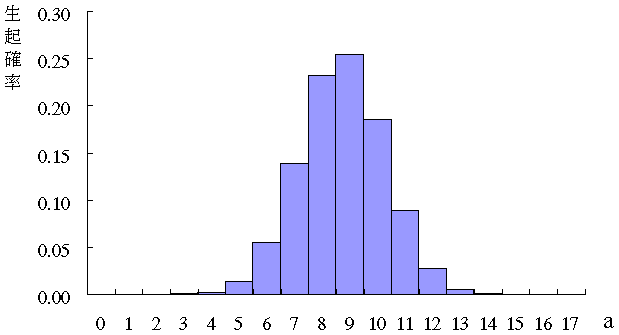
この matlab 関数 は x の 2 つのカテゴリカル変数の間に非無作為な関連性があるという対立仮説に対して、非無作為な関連性がないという帰無仮説のフィッシャーの正確確率検定を行なった結果を返しまフィッシャーの正確確率検定（フィッシャーのせいかくかくりつけんてい、英 Fisher's exact test ）は、標本の大きさが小さい場合に、2つのカテゴリーに分類されたデータの分析に用いられる統計学的検定法である 。 フィッシャーの直接確率検定ともいう。名称は考案者ロナルド・フィッシャーなお正確確率においては片側は両側を2でわった値ではない。片側p値は観測値以下（または以上）の生起確率をすべて足したものである。 pvalue ← 1 sum(実測値の生起確率よりも大きい確率) 2*2(自由度1)のクロス集計表で正確確率を求める関数サンプル

 Excel VBAでフィッシャーの正確検定ができる関数を作ってみた2 静粛に、只今統計勉強中 前回、『 Excel で学ぶコレスポンデンス分析』を参考に、 Excel VBA で2×2表専用のフィッシャーの正確検定ができる関数を作りました。 今回は、作った関数を実際に使っ生起確率 $\\displaystyle = \\frac{ e!フィッシャーの正確確率検定2×2 Fisher's test 2行×2列の分割表（クロス集計表）から独立性を検定する手法です。 組み合わせを直接計算して確率を求めるのが特徴です。Videos you watch may分布の差の検定（独立性の検定） 独立性の検定（k×m 分割表） 独立性の検定（2×2 分割表） フィッシャーの正確確率検定（直接確率）

Rの練習 Fisher Test でメモリが足りなくなる Statsbeginner 初学者の統計学習ノート

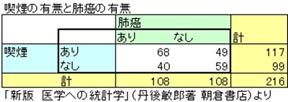
フィッシャーの直接確率検定 統計解析ソフト エクセル統計

 Rの練習 fishertest ()でメモリが足りなくなる ちょっとしたデータをカイ二乗検定しようとすると、往々にして、期待度数が5に満たないセルが存在するせいで警告が出ます。 > print ( d) Group1 Group2 Item1 3 2 Item2 9 12 Item3 32 41比率の差の検定 フィッシャーの正確確率検定 対応のある場合 マクネマー検定 3群以上の比率の差 対応のない場合 フィッシャーの正確確率検定 対応のある場合(2値型変数) コクランのq検定 はじめに みなさんは"フィッシャーの正確確率検定"と"カイ2乗検定"という言葉を聞いて, どちらの方がより正確そうだと思いますか？ 答えは, 「2者は比較できない」です。 しかし, 生物統計ではこの2者のどちらかを使うかがしばしば問題になり, 「カイ2乗検定が役に立たないシ

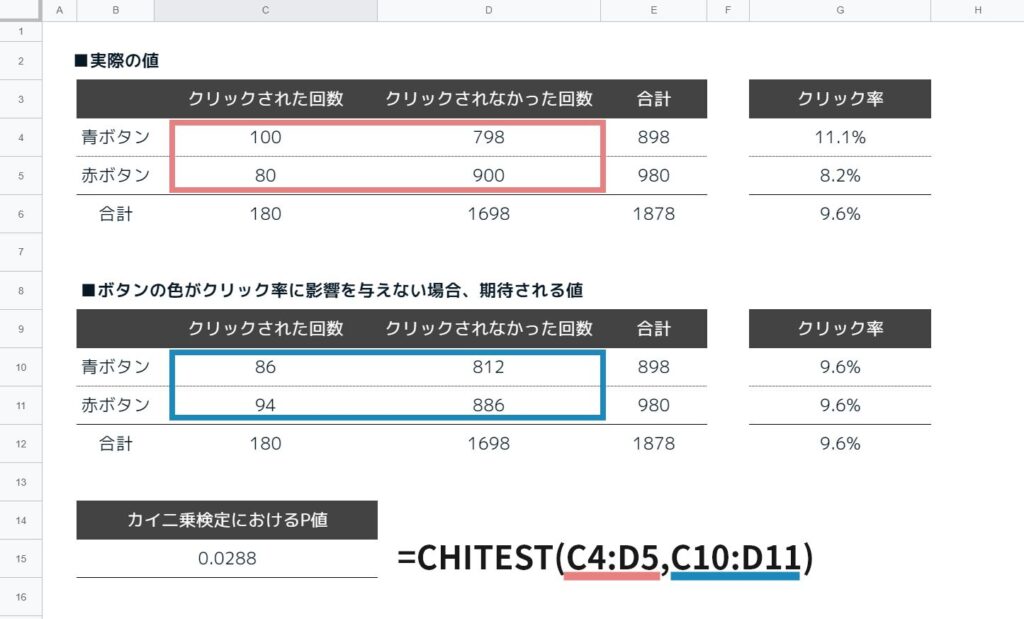
その分析結果は偶然ではありませんか カイ二乗検定 独立性の検定 で確かめる Chitest関数 Zizi Tips

カイ二乗 X2 とfisherの検定 化審法 動物数 5 Vs 5 7 Vs 7 Or 12 Vs 12を考える Ppt Download

フィッシャーの直接確率検定 χ 2 検定は近似的な方法である．正確な計算を行う場合は，フィッシャーの直接確率検定を用いる．関数は fishertest() を使い，引数には 2×2 の行列を与えればよい． 今回は「2群間を比べる」検定のひとつである 「カイ2乗(χ 2)検定」「フィッシャー(Fisher)の正確検定（直接確率法）」 について実践してみたいと思います。 「カイ2乗(χ 2)検定」は聞いたことありますか？ 学会発表などでも使いやすい検定ですので、聞いたことがある方も多いとエクセルのvbaを使って作成した、フィッシャーの直接確率計算のプログラムです。 使い方 1終了したいときには、「excel終了」ボタンを押して下さい。 2プログラムをアンインストール(削除)するときには、ホルダー全体を削除して下さい。 注意事項

統計初心者です フィッシャーの正確確率検定でエクセルでp値を求めたら1 00 Yahoo 知恵袋

フィッシャーの正確確率検定とは カイ二乗検定との違いをわかりやすく いちばんやさしい 医療統計

 おすすめタグ タグについて よく使うタグ すべてのタグを表示 ブックマークを追加 Fisher の正確確率検定を Excel を使って計算する 2 users aoki2sigunmauacjp 禁止事項と各種制限措置について をご確認の上、良識あるコメントにご協力ください 0 / 100 入力X に対するフィッシャー変換の値を返します。 この関数を使うと、非対称分布を正規分布に変換することができます。 この関数は、相関係数の仮説検定を行うときに使用します。 書式 fisher(x) fisher 関数の書式には、次の引数があります。 x 必ず指定します フィッシャーの正確検定 (Fisher's exact test）は、フィッシャーの直接確率法とも呼ばれるもので、2x2の分割表が得られたときに有意差があるかないかを調べるときに使われます。 χ2乗検定も同じ目的で使われますが、違いはデータの個数が少ないかどうか

Ezrでfisherの正確検定を行う方法 深kokyu

R でフィッシャー正確確率検定をし さらに多重比較を行う方法 高知の田舎で耕すデータサイエンス農家のブログ

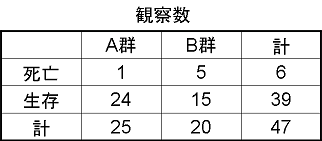
 Rでは、デフォルトの関数を用いて実行可能 まず、検定したいデータ（実際に観測されたデータ）を読み込みます。 > mx = matrix(c(1, 6, 5, 2), nrow=2, byrow=T) > mx ,1 ,2 1, 1 6 2, 5 2 フィッシャーの正確確率検定は、以下のように実行するだけです。実際、片側検定と両側検定ではどう違うかというと、両側検定におけるP値005は、片側0025になりますが、片側検定では片側のみで005なので、 当然片側検定の方が有意差が出やすくなります。 フィッシャーの正確確率検定の場合コクランの q 検定 （プロシージャ版） 順位相関係数 ★ スピアマンの順位相関係数を求める関数 ★ ケンドールの順位相関係数を求める関数;

遺伝統計学 夏の学校 大阪大学17講義資料 統計学入門

統計一口メモ 第8話 Fisher正確検定は片側 それとも両側 安全性評価研究会

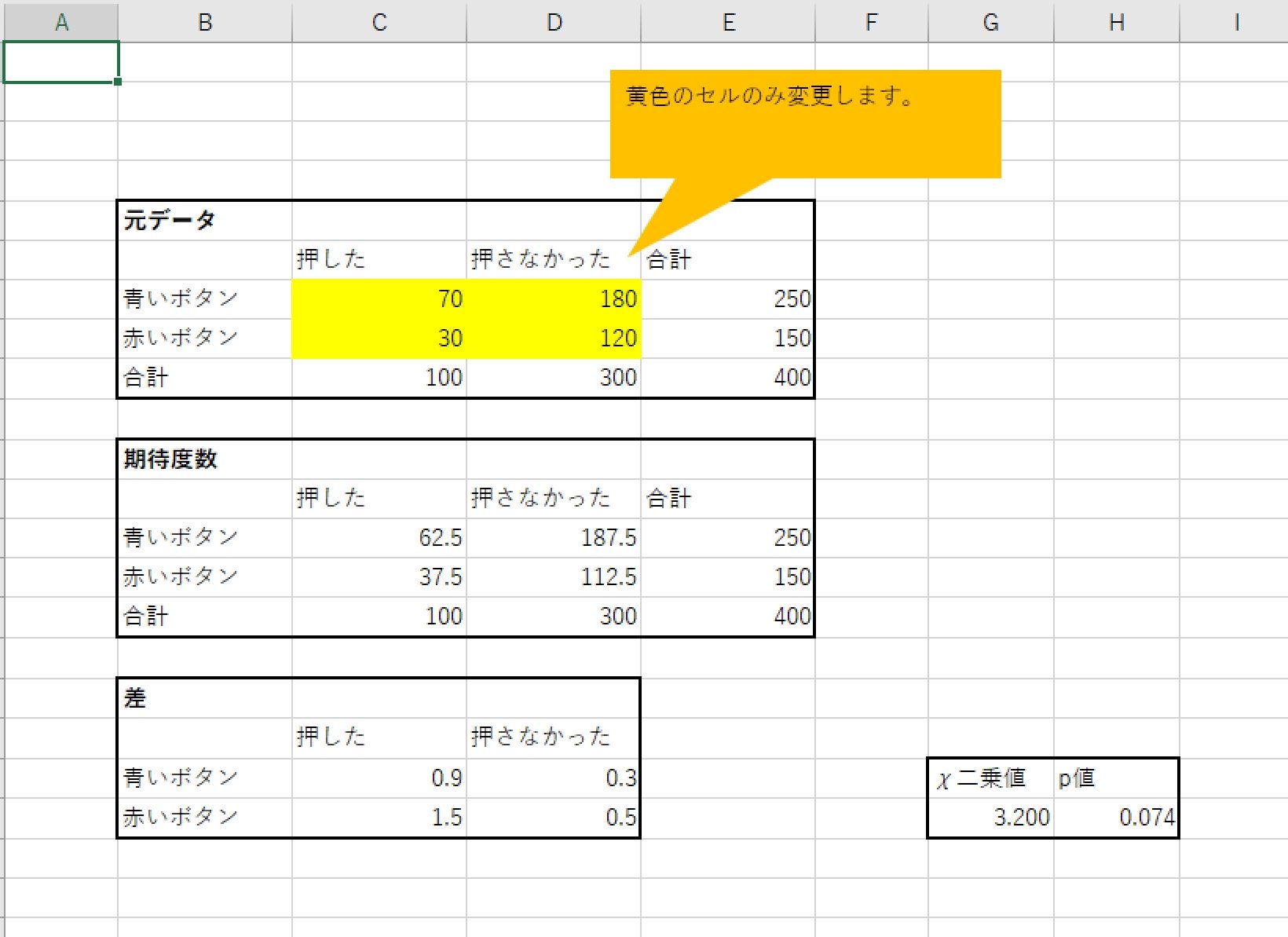
 ホーム > 統計・データ解析 > Fisherの正確検定かカイ2乗検定か 黒木玄さんが追試をしてくださって，このページの ECDF for chisqtest(correct=T) の図が微妙に違うと教えていただきました。 図のタイムスタンプは ですが，chisqtest() の仕様が変わったとも考えられず，おそらく私の適合度検定（4） 仮説検定を考えるにあたり，最も困難な部分は検定統計量が帰無仮説の下で従う確率分布の導 出である．検定統計量𝑋02が帰無仮説の下で自由度 −𝑟−1のカイ二乗分布に従うことを示す （ =2,𝑟=0の場合） 𝑋0 2= 𝑋1− 2フィッシャーの正確確率検定でやっていることは、カイ二乗検定と一緒 フィッシャーの正確確率検定。 t検定とかf検定とかと比べると、やたら長い名前です。 その仰々しい名前から、「なんか難しそう・・・」とあなたは思っているかもしれませんね。

Fisherの正確確率検定 は正確ではない

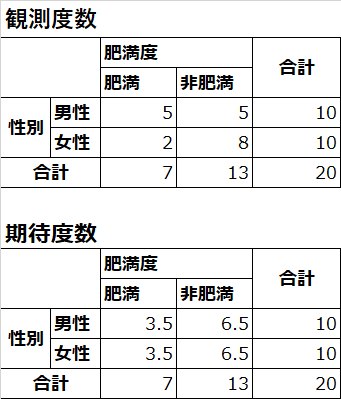
R 栄養統計 性別と肥満度に関係があるか カテゴリデータの栄養統計 みんな栄養に頼りすぎてる

説明 両側確率p値の求め方については,Pearsonのカイ二乗法とFisherが示した方法があります。 2つの方法によるp値は,ほとんどの場合に同じですが,異なることもあります。 jsSTARではFisherが示した方法で求めています。 オッズ比検定では,いずれかの観測値に 0 ftestの値は両側確率であるため、片側確率は半分の"0275"になります。有意水準を5%とすると、0275 > 005 となり、2つのグループでの有意差は無いと判断でき、仮説は棄却されず、分散は同じであると言えます。 f検定をする 続いて、先の条件の値に変更します。本サイトは、2way Contingency Table Analysisを著者の許可を得て日本語翻訳したものです(07年)。 このページは2×2テーブルから様々な統計を計算します。 イエーツ補正のカイ2乗検定、MantelHaenszel検定、Fishser正確確率検定、その他の様々な2x2分割に関連した検定について計算するもの

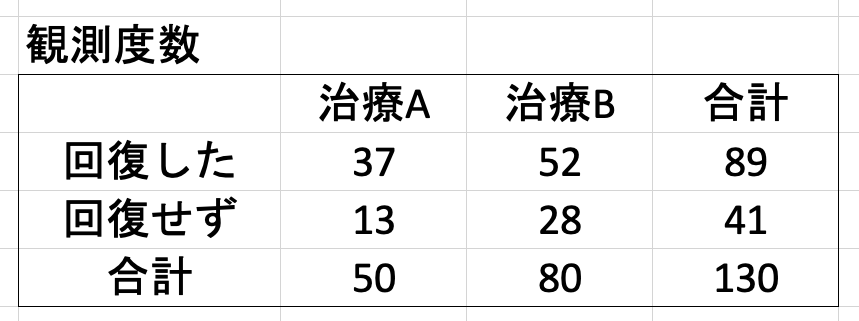
カイ二乗検定 独立性の検定 原理と Excel による解析

フィッシャーの正確確率検定 情報リテラシー

フィッシャーの正確確率検定（フィッシャーのせいかくかくりつけんてい、英 Fisher's exact test ）は、標本の大きさが小さい場合に、2つのカテゴリーに分類されたデータの分析に用いられる統計学的検定法である 。 フィッシャーの直接確率検定ともいう。名称は考案者ロナルド・フィッシャー

Excel Vbaで３群以上の比率の差の多重検定ができるマクロを作ってみた１ 静粛に 只今統計勉強中

フィッシャーの正確確率 株式会社ダイナコム

Matlab フィッシャーの正確確率検定はカイ2乗検定より本当に正確か Qiita

Fisher正確検定 Appkaiju

Rより Fisher直接確率検定を実施するとオッズ比が0 0 Yahoo 知恵袋

フィッシャーの正確確率検定とは カイ二乗検定との違いをわかりやすく いちばんやさしい 医療統計

フィッシャーの正確確率検定とは何 Weblio辞書

統計一口メモ 第8話 Fisher正確検定は片側 それとも両側 安全性評価研究会

カイ二乗検定 独立性の検定 Kota S Lab

統計 Fisher検定で多重比較する場合について 3群の独立性の Yahoo 知恵袋

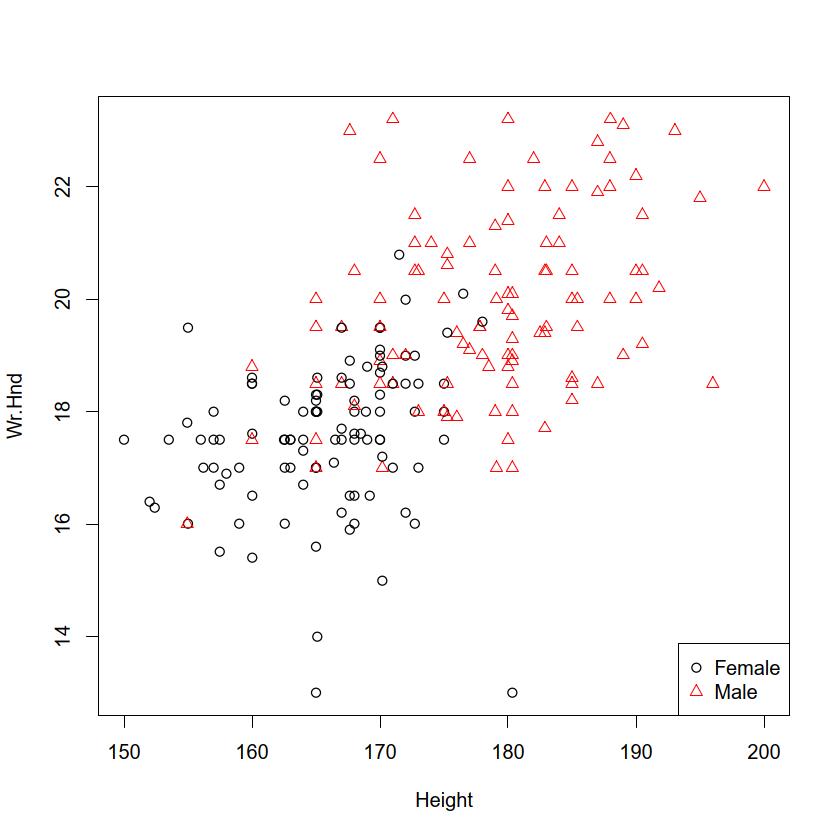
保健 医療研究の進め方入門 Rとezrを用いて 保健学共通特講iv Viiiテキスト Rev 1 0 1

Ezrでカイ二乗検定とフィッシャーの正確検定を実施する方法 Youtube

Excelの分析ツール 3 ブログ 統計web

Ezrでfisherの正確検定を行う方法 深kokyu

スポーツ健康科学部ブログ あいコアの星 立命館大学

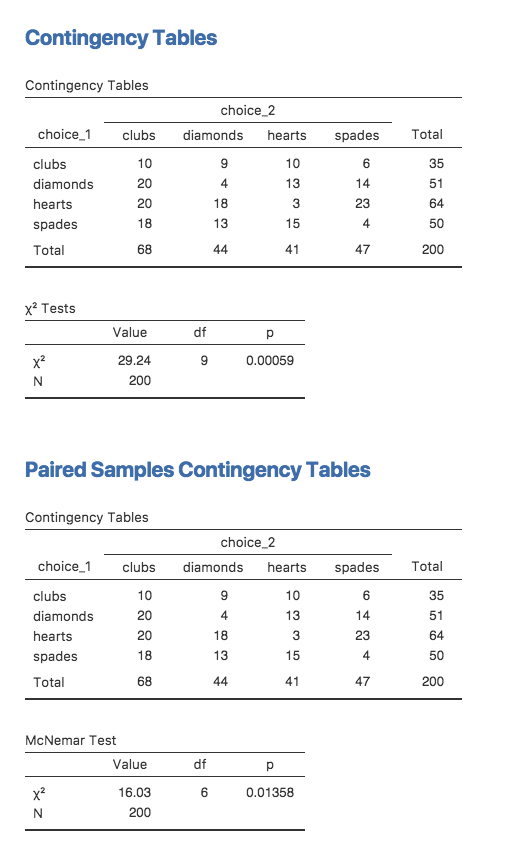
第10章 カテゴリーデータの分析 Jamoviで学ぶ心理統計

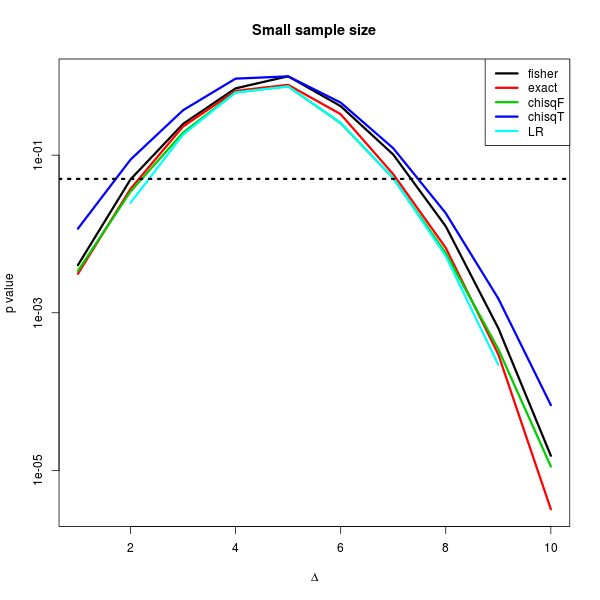
フィッシャーの正確確率検定とカイ自乗検定と尤度比検定 驚異のアニヲタ社会復帰の予備

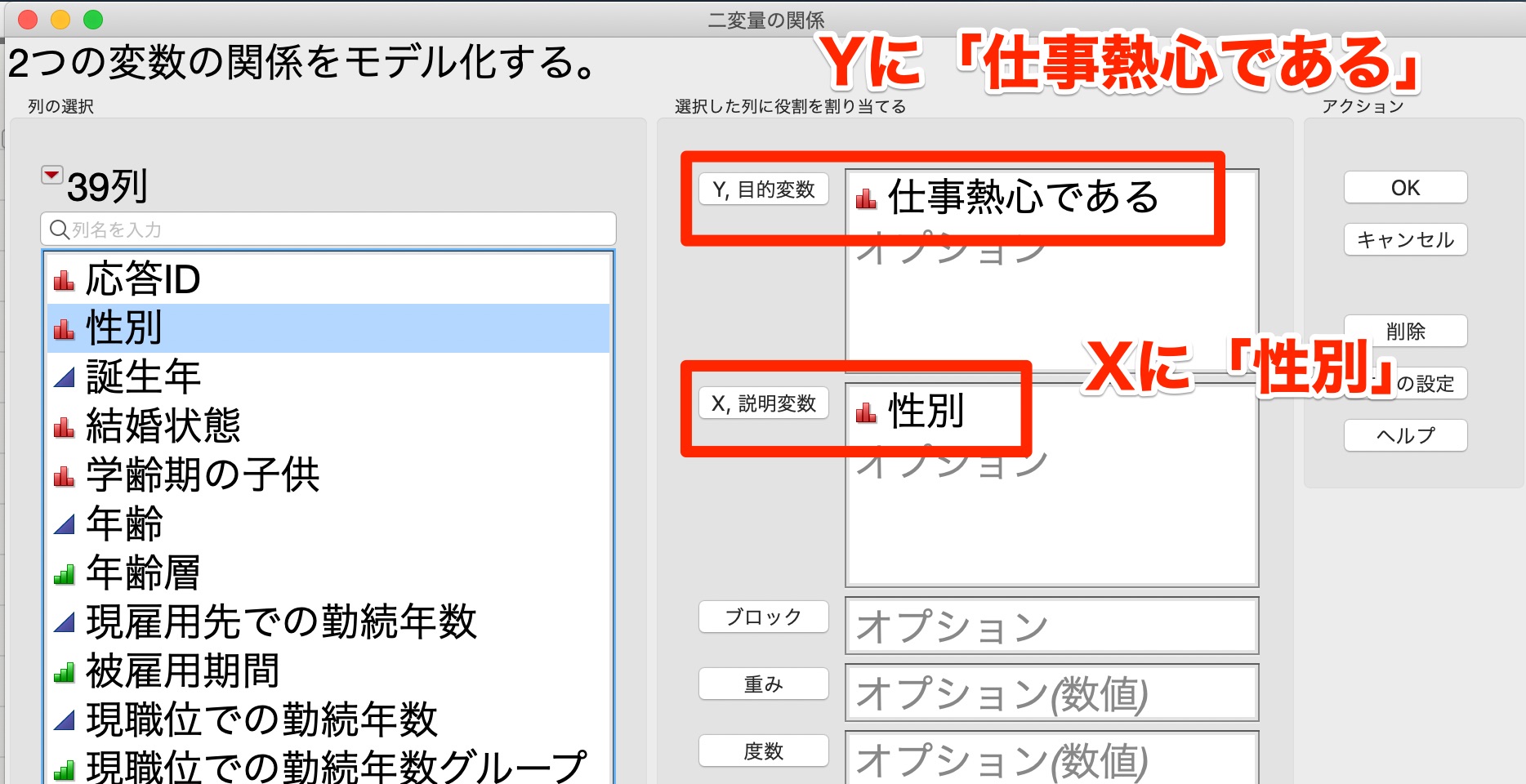
Jmpでカイ二乗検定を実施する方法 フィッシャーの正確確率検定も いちばんやさしい 医療統計

フィッシャーの正確確率検定 情報リテラシー

スポーツ健康科学部ブログ あいコアの星 立命館大学

Fisher正確検定 Appkaiju

Fisherの正確確率検定 Study Channel

Fisherの正確確率検定について質問です Jmpという統計ソフトを用い 統計学 教えて Goo

Fisherの正確確率検定 Study Channel

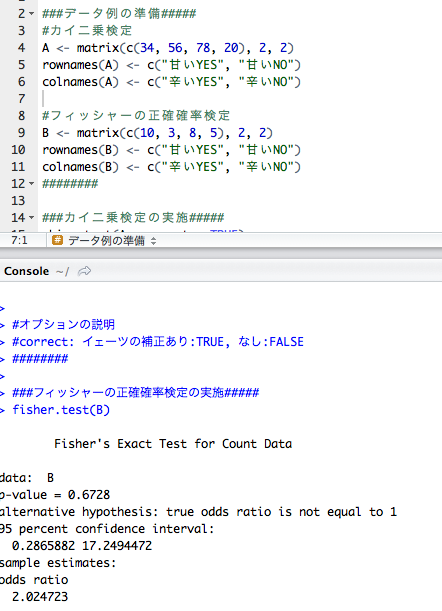
Rとウェブ解析 カイ二乗検定とフィッシャーの正確確率検定のコマンド紹介

独立性のカイ二乗検定 例題を用いてわかりやすく解説 Avilen Ai Trend

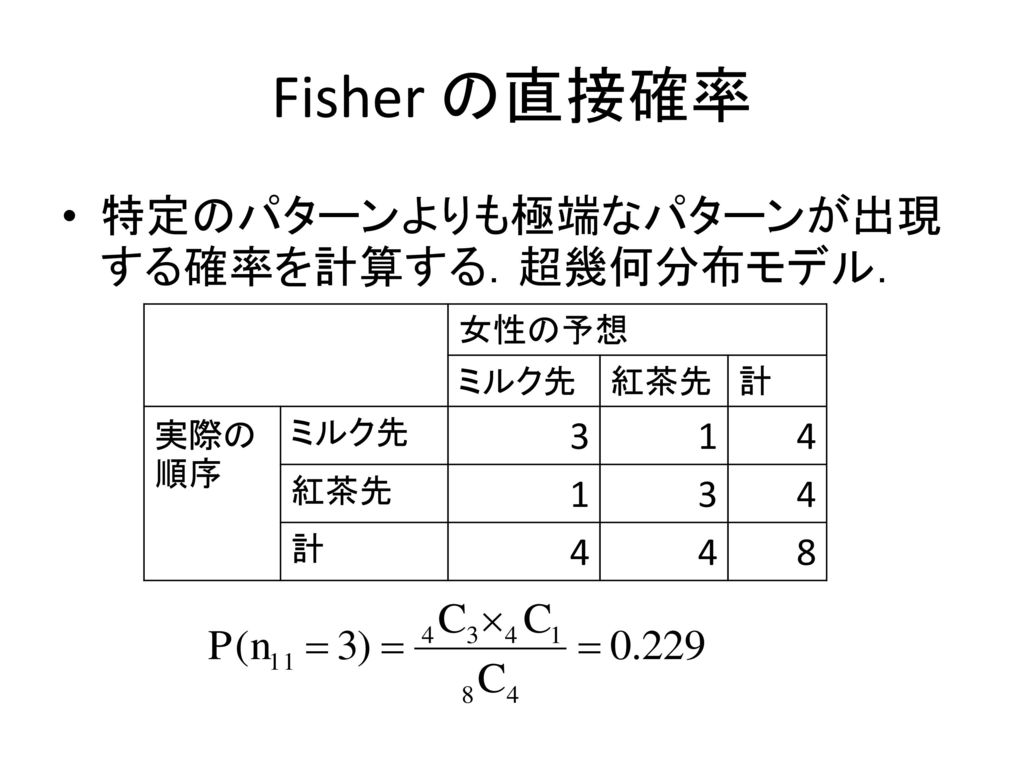
寺尾 敦 青山学院大学社会情報学部 Fisher の直接確率法 寺尾 敦 青山学院大学社会情報学部 Ppt Download

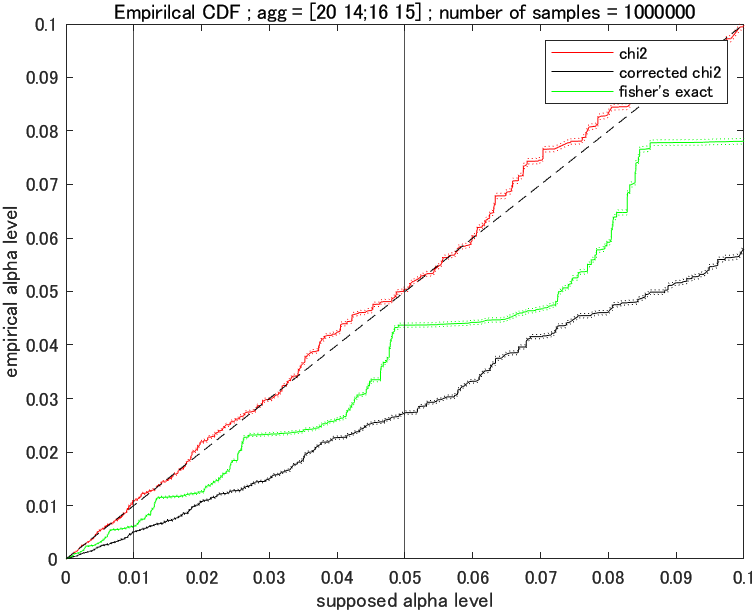
Matlab フィッシャーの正確確率検定はカイ2乗検定より本当に正確か Qiita

統計的テキスト解析 11 テキストにおける分割表の分析

X2乗検定とfisher正確確率検定 X2乗検定の不適切使用をしていませんか Earlの医学ノート

クロス集計表から分析する 1 ブログ 統計web

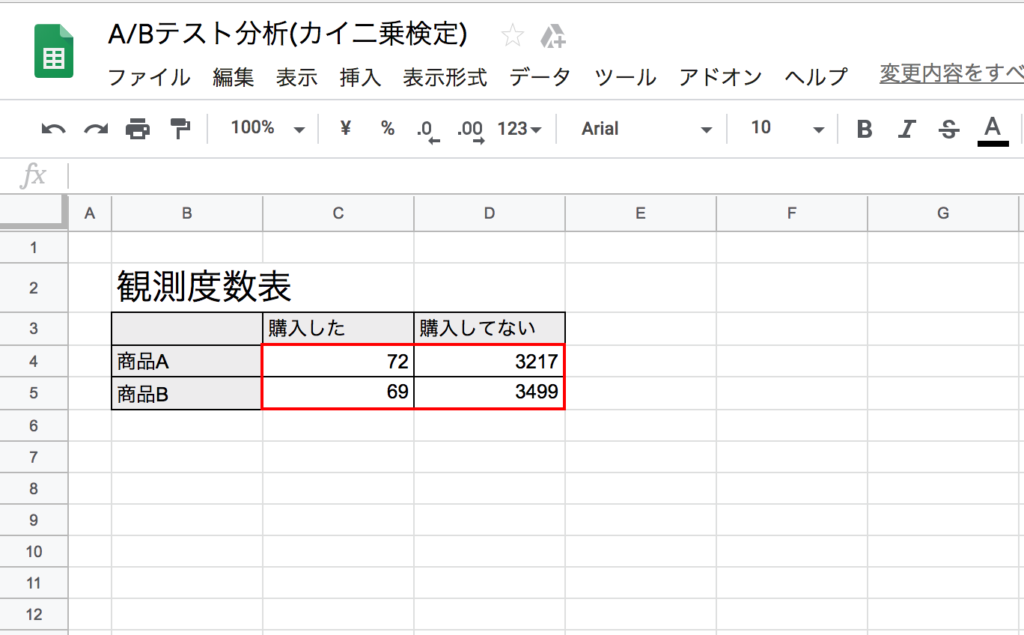
スプレッドシートでピアソンのカイ二乗検定 独立性の検定 を行う方法 たぬハック

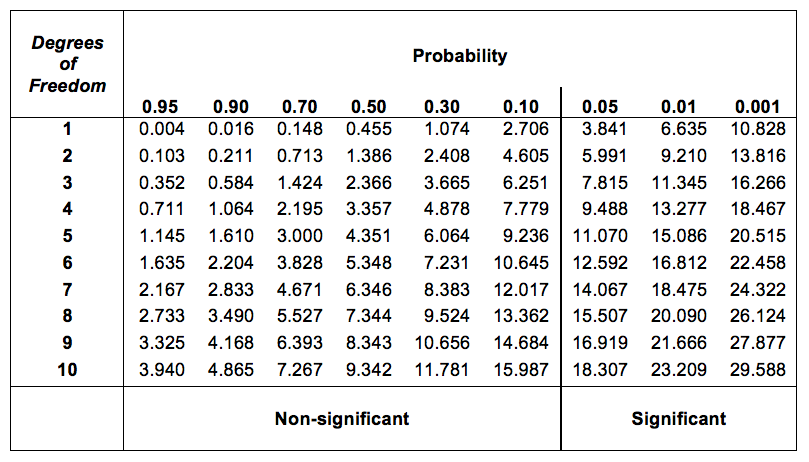
第10章 カテゴリーデータの分析 Jamoviで学ぶ心理統計

Excel Vbaでフィッシャーの正確検定ができる関数を作ってみた２ 静粛に 只今統計勉強中

フィッシャーの正確確率検定 情報リテラシー

Fisherの直接確率検定を計算するには Improve Society

Rによる関数グラフの作成

Fisherの直接検定のやり方 実験データの具体的な解析方法

ヤフオク 3251 Ssri エクセル統計10

2

R 栄養統計 性別と肥満度に関係があるか カテゴリデータの栄養統計 みんな栄養に頼りすぎてる

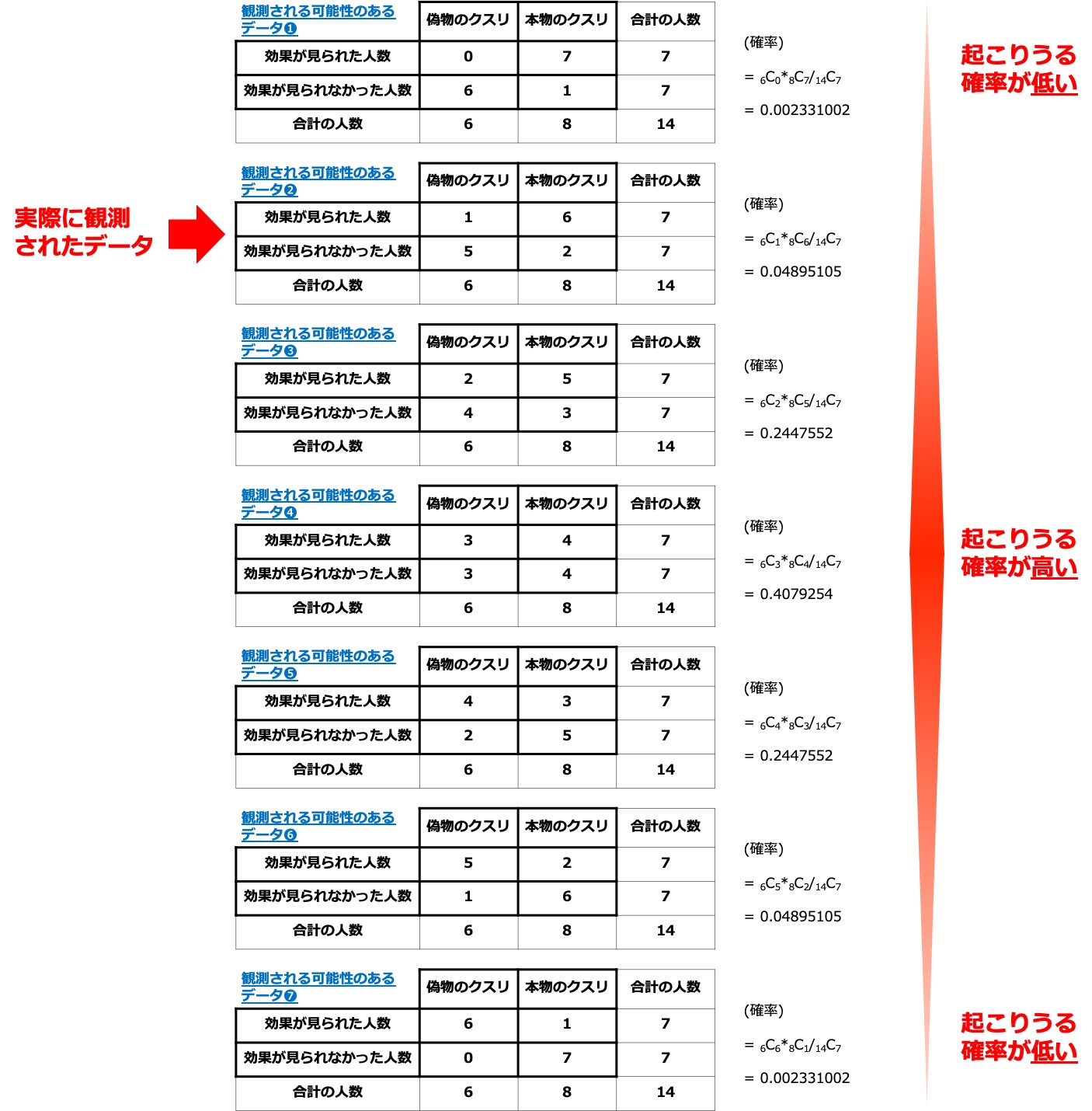
フィッシャーの正確確率検定をわかりやすく解説 Rを使って検定 Mi Chan Nel みっちゃんねる

Rでフィッシャーの正確確率検定 そのまま使える自作関数例 Avilen Ai Trend

Excel Vbaでフィッシャーの正確検定ができる関数を作ってみた１ 静粛に 只今統計勉強中

独立性のカイ二乗検定 例題を用いてわかりやすく解説 Avilen Ai Trend

Excel 中央値や平均値の条件指定など統計に使える関数7つ紹介 Youtube

フィッシャーの正確確率検定 情報リテラシー

カイ二乗検定 独立性の検定 原理と Excel による解析

2

Excel Vbaでフィッシャーの正確検定ができる関数を作ってみた２ 静粛に 只今統計勉強中

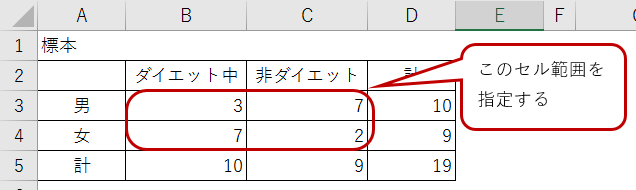
Excel Vbaでフィッシャーの正確検定ができる関数を作ってみた２ 静粛に 只今統計勉強中

Rを使った分析 カイ2乗検定 外国語教育研究ハンドブック外国語教育研究ハンドブック

統計一口メモ 第8話 Fisher正確検定は片側 それとも両側 安全性評価研究会

フィッシャーの正確確率検定について教えてください 表は ある病院 Yahoo 知恵袋

その分析結果は偶然ではありませんか カイ二乗検定 独立性の検定 で確かめる Chitest関数 Zizi Tips

Rでyouden Indexを用いたroc曲線の最適カットオフ Avilen Ai Trend

Spssでカイ二乗検定 フィッシャーの正確確率検定との違いやp値の解釈も いちばんやさしい 医療統計

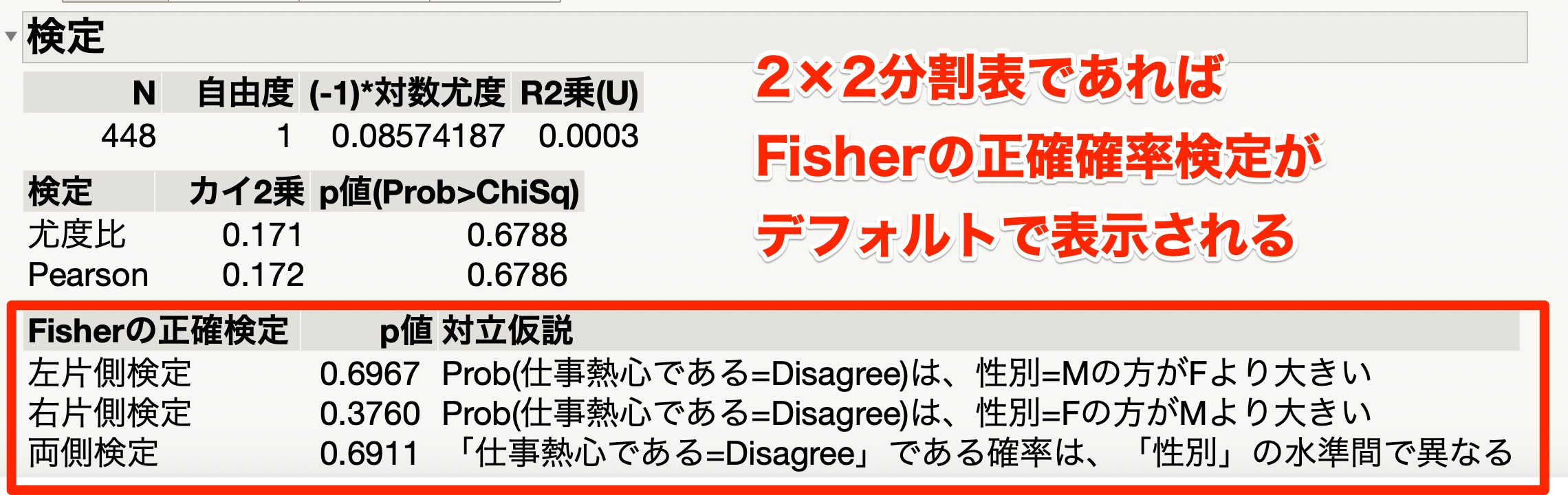
Jmpでカイ二乗検定を実施する方法 フィッシャーの正確確率検定も いちばんやさしい 医療統計

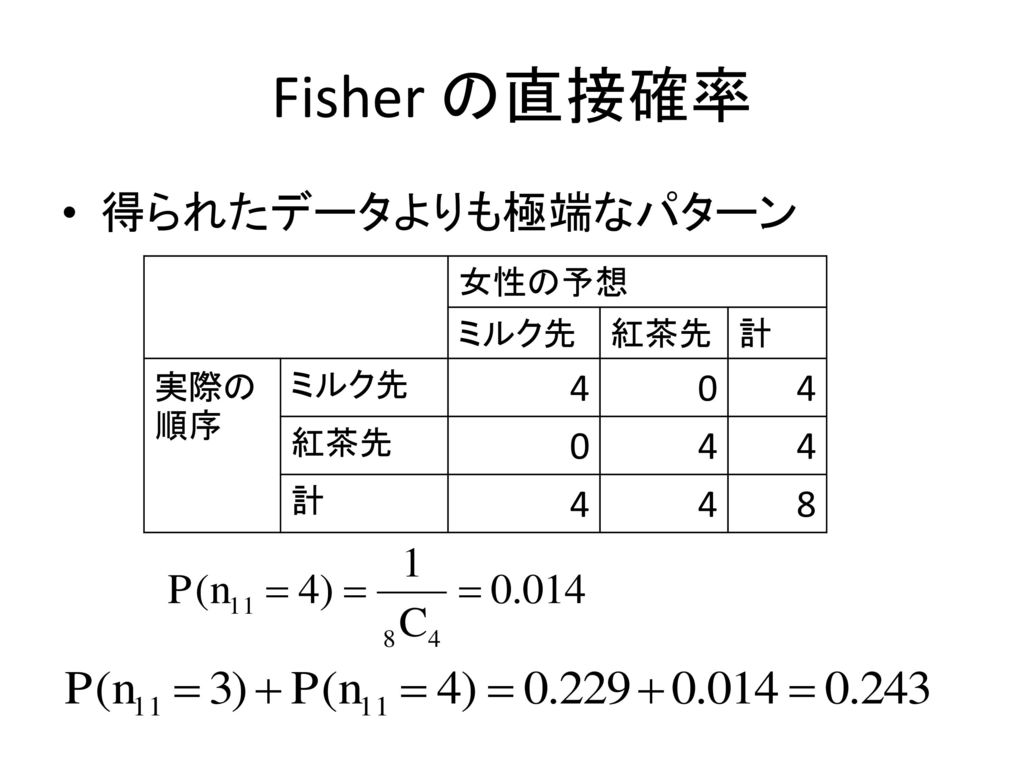
寺尾 敦 青山学院大学社会情報学部 Fisher の直接確率法 寺尾 敦 青山学院大学社会情報学部 Ppt Download

Fisher S Exact Test

Excelで学ぶ統計解析本格入門 日花 弘子 本 通販 Amazon

カイ2乗検定と Fisherの正確検定チュートリアル Xlstat Support Center

クロス集計表で独立性検定のカイ2乗検定を行いましたが いくつかのセルは期待度数が5未満ですと表示されてしまいます

Fisherの直接法 統計学備忘録 R言語のメモ

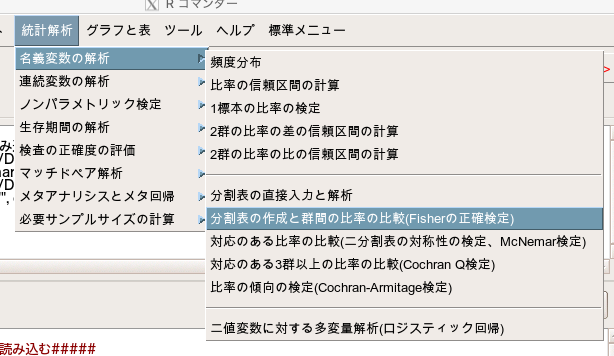
Ezrでカイ二乗検定とフィッシャーの正確検定の実施方法 分割表でクロス集計 いちばんやさしい 医療統計

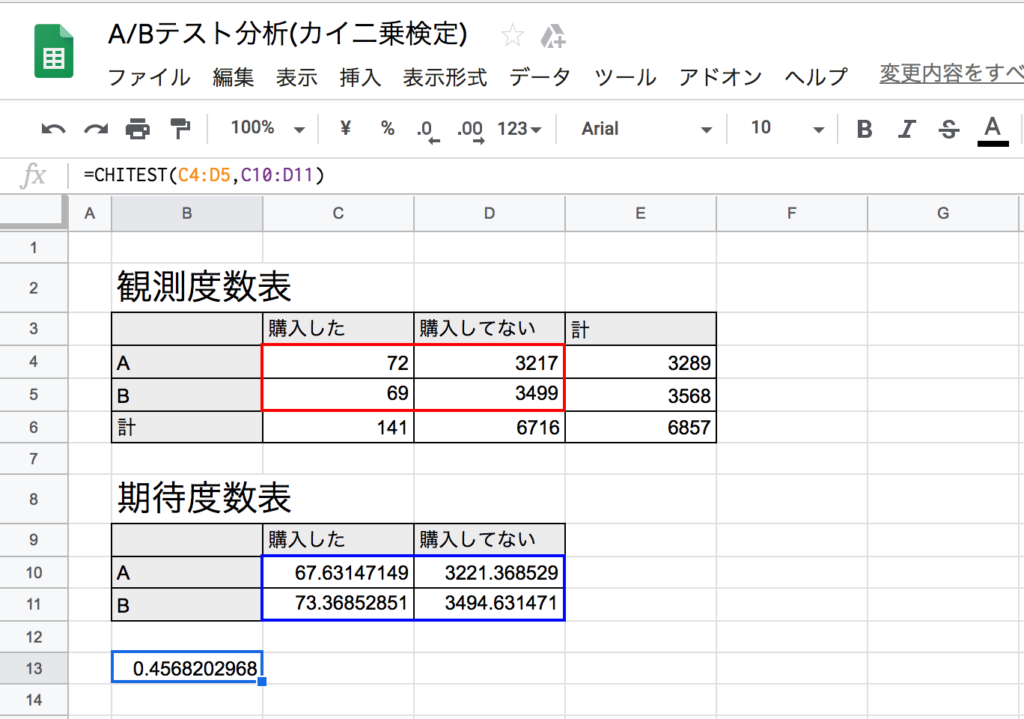
スプレッドシートでピアソンのカイ二乗検定 独立性の検定 を行う方法 たぬハック

Excel Vbaでフィッシャーの正確検定ができる関数を作ってみた１ 静粛に 只今統計勉強中

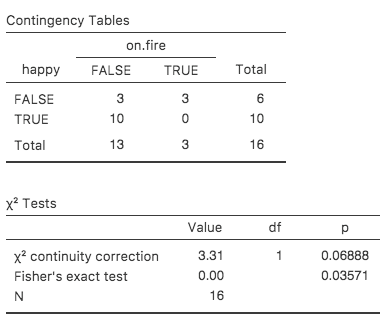
第10章 カテゴリーデータの分析 Jamoviで学ぶ心理統計

Lobbrownp 78 Adjustments Administered Administration Administrative Administrators Admirable

クロス集計 Spssの使い方

カイ二乗分布のわかりやすいまとめ Avilen Ai Trend

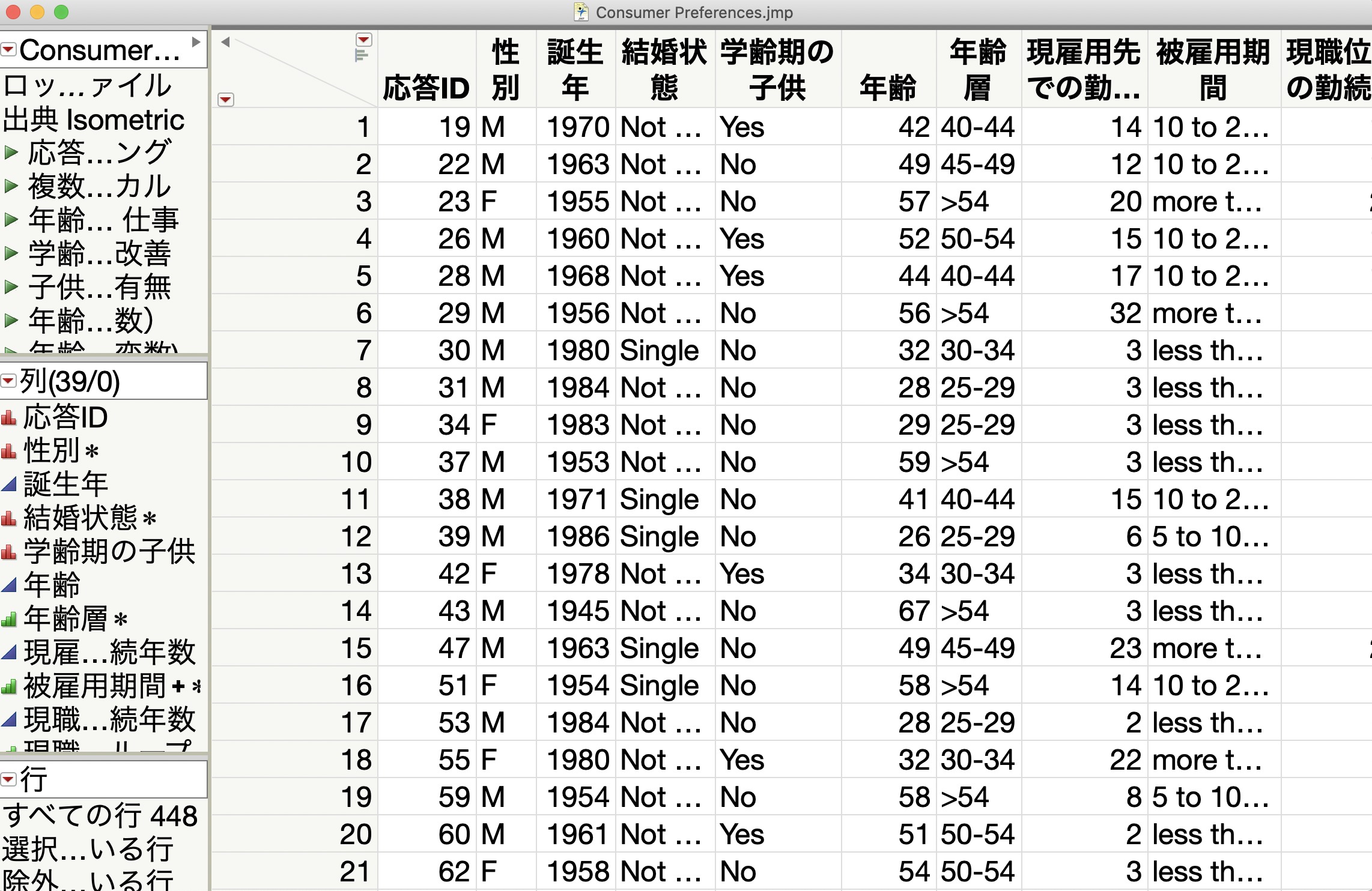
Jmpでカイ二乗検定を実施する方法 フィッシャーの正確確率検定も いちばんやさしい 医療統計

エクセルを使ったフィッシャーの正確確率検定 統計学初学者です エクセル Yahoo 知恵袋

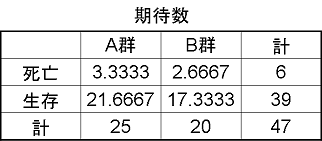
X2乗検定とfisher正確確率検定 X2乗検定の不適切使用をしていませんか Earlの医学ノート

フィッシャーの正確確率検定をわかりやすく解説 Rを使って検定 Mi Chan Nel みっちゃんねる

フィッシャーの正確確率検定 情報リテラシー

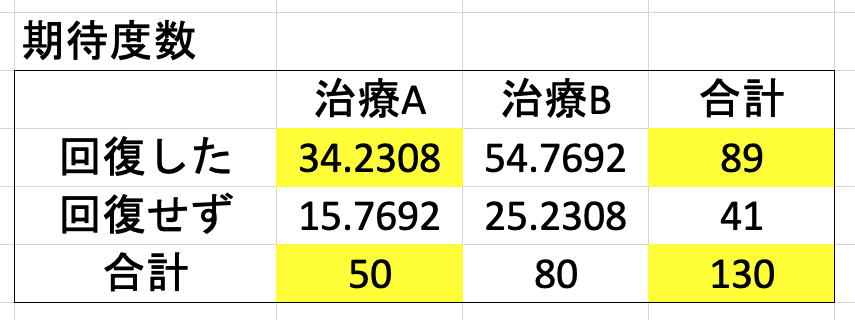
カイ二乗検定 独立性の検定 原理と Excel による解析

カイ2乗検定と Fisherの正確検定チュートリアル Xlstat Support Center

カイ二乗検定 Logics Of Blue

Spssでx二乗検定をやってみる 出力結果の読み方と意味を基本から丁寧に解説します フィッシャーの正確確率検定についても説明します Youtube

クロス集計 Spssの使い方

Excel関数一覧 読み方 語源含む Excelを制する者は人生を制す No Excel No Life

フィッシャーの正確確率検定とは カイ二乗検定との違いをわかりやすく いちばんやさしい 医療統計

統計 Fisher S Exact Test こちにぃるの日記

フィッシャーの正確確率検定

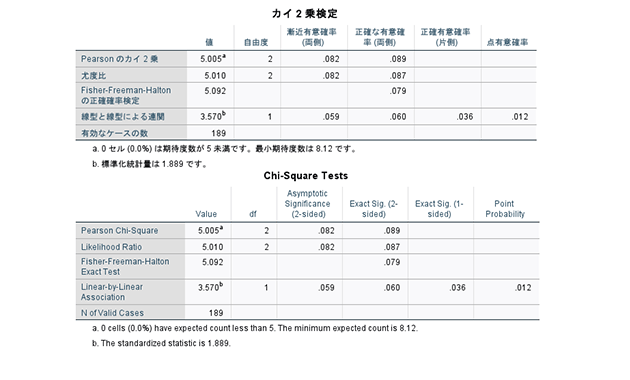
Ibm Spss Exact Tests 製品情報 小サンプルでの正確有意確率

統計講座